实习中的idea

1.如何根据市场交易规则（最小交易单位）来执行计算出的交易信号。

(考虑交易手数的话，需要解一个以最小化持仓误差为目标函数的、以总资金为硬约束的整数线性规划问题)

2.利用alpha值生成持仓信号

在利用经过行业市值中性化、过滤掉涨跌停的final alpha values计算对应的持仓比例、多空持仓情况时，可以考虑使用power rank。

def cal_cs_rank(x, maxvalue=None,minvalue=None):
    '''
    部分经过删除处理
    '''
    res = np_nan_array(shape = (x.shape[0],), dtype="float64")
    res = (res - np.nanmin(res)) / (np.nanmax(res) - np.nanmin(res)) * (maxvalue - minvalue) + minvalue
    return res

具体是把因子先利用rank函数展成(-1,1)的均匀分布形式，再根据对于头部权重的考虑，对展开后的值取3次方、5次方。

1次方就是均匀分布

plot_distribution(Analyzer.industry_analyze_detail('2021-03-29')['factor'].values,'power=1')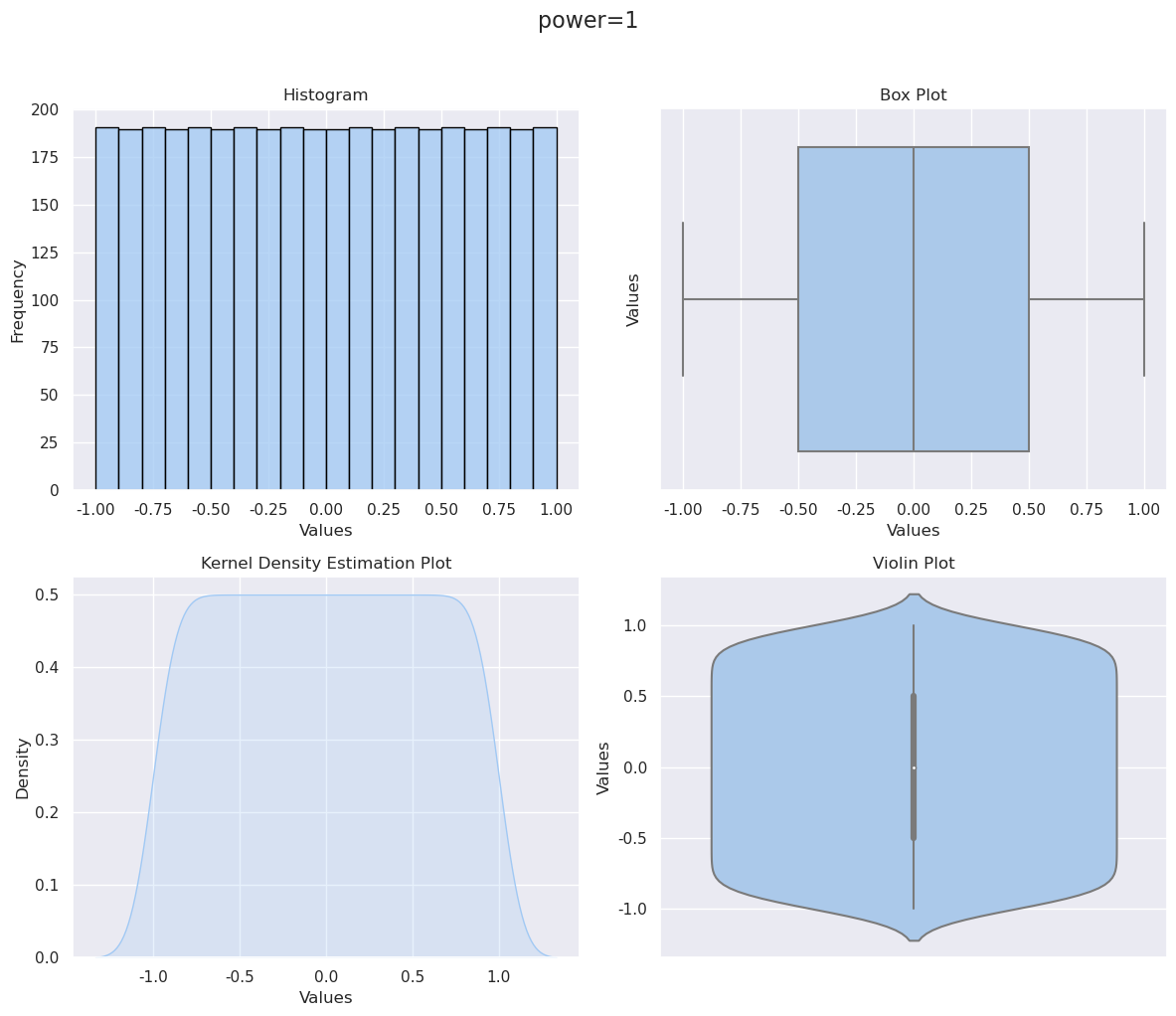

取奇次幂可以放大头部权重

power=3	power=5
`plot_distribution(tmp**3,'power=3')`	`plot_distribution(tmp**5,'power=5')`

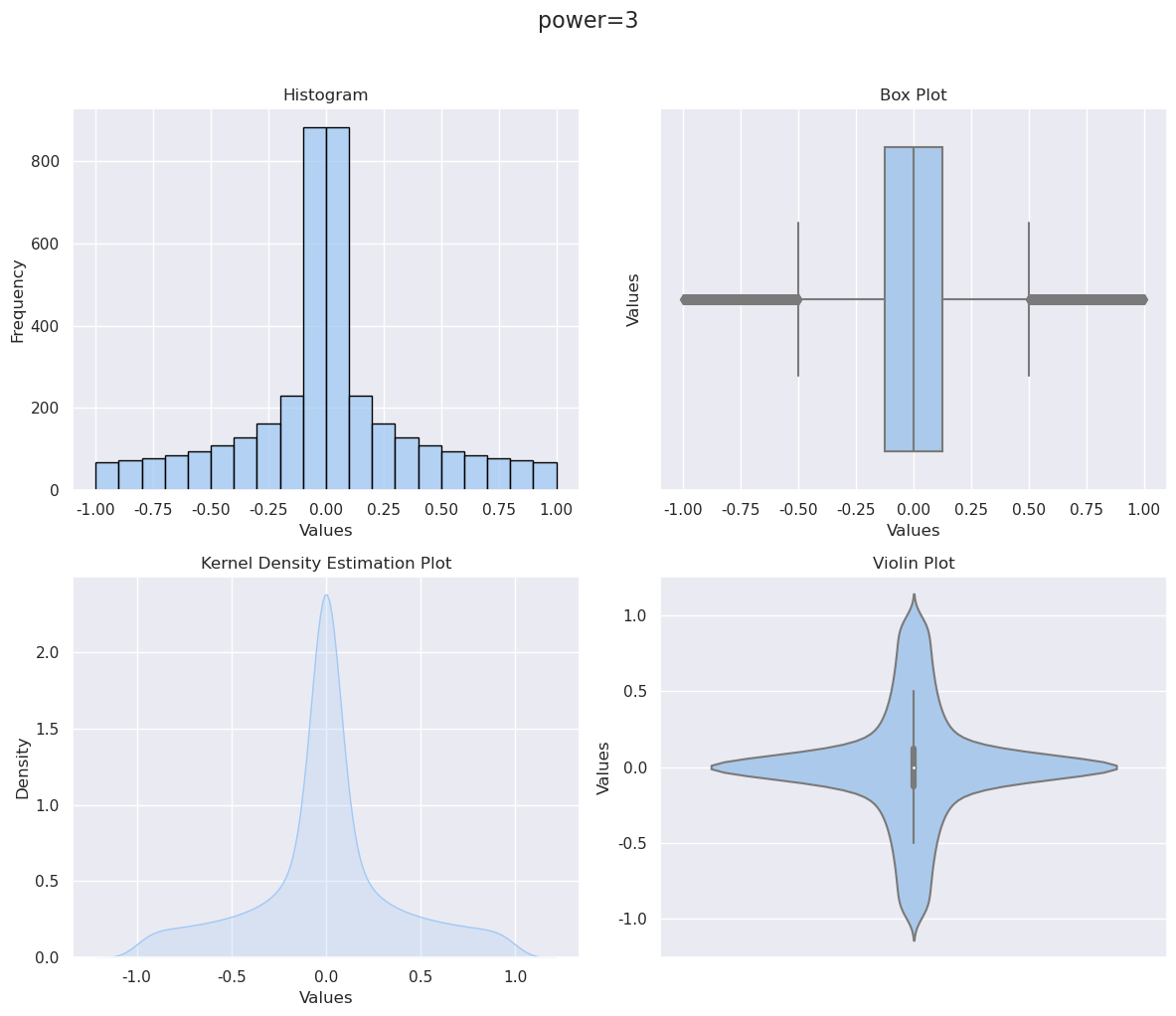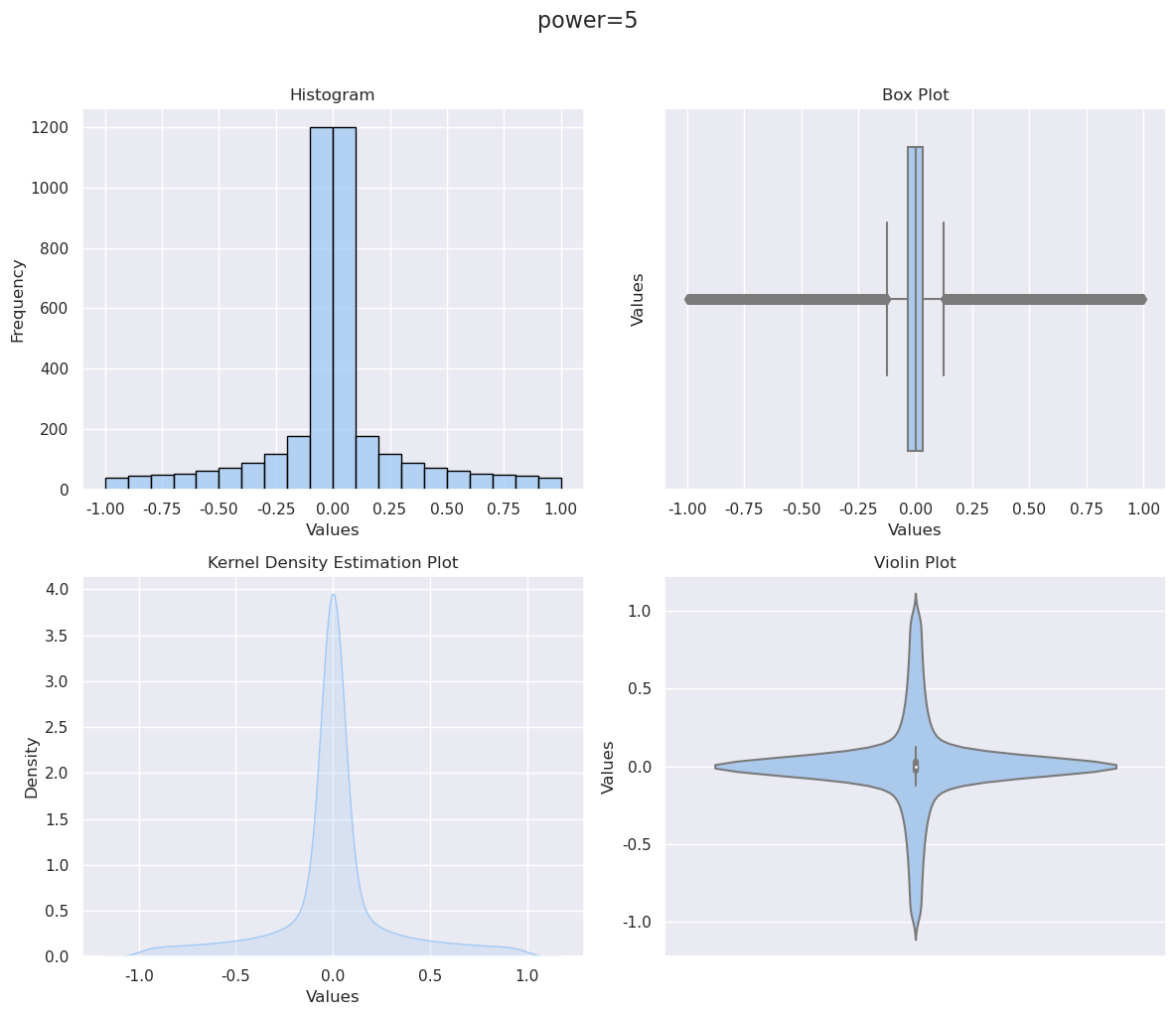3.回测计算的是单利

df['ac_returns'] = df['returns'].cumsum()

4.因子组合优化的最简单形式

本报告根据模型滚动训练和预测的结果，将所有测试集上的预测结果作为最终合成的打分输出用于策略组合构建，每5个交易日进行一次调仓，仓位调整逻辑是在一定的约束条件下最大化加权模型预测打分值，同时限制组合的换手。每次调仓日的模型预测输出的股票得分向量记为 $\text{score}_{t}$，当期目标权重向量记为 $w_t$，优化目标方程为: \[ \begin{aligned} & \max \left(\sum_{i=1}^n w_{t, i} * \text { score }_{t, i}-\alpha\left|w_t-w_{t-1}\right|\right) \\ & \text { s.t }\left\{\begin{array}{l} -0.005 I \leq w_t-w_{\text {benchmark }} \leq 0.005 I \\ \sum_{i=1}^n w_{t, i}=1 \\ w_t \geq 0 \end{array}\right. \end{aligned} \] 其中，$\alpha$用于约束换手率，取值 0.05 ；$ w_{benchmark}$为股票的基准权重向量； 1 是所有元素为 1 的长度为 $w_t$的向量，个股权重相对于基准成分股权重的偏离限制在正负 $0.5 \%$ 内。策略每 5 个交易日在收盘后通过上述优化目标和条件求解权重。