《统计学习》学习记录
作为非科班出身的金数人,在学习机器学习模型时我发现自对一些最基础、最本质的概念理解不够深入,所以打算写一篇blog,记录一下自己在学习的时候遇到的零零散散的问题。
1.极大似然估计(MLE)和损失函数的关系
- 若变量服从高斯分布,MLE的结果是OLS
- 若变量服从伯努利分布,MLE的结果是logistic回归
- 若变量服从多项式分布,MLE的结果是softmax
2.当我们对损失函数正则化时,我们在做什么?
做正则化的目的就是为了提高训练出模型的泛化能力。影s响模型泛化能力的是权重 \(w\) 和偏置 \(b\) 。
2.1 拉格朗日对偶角度
所谓正则化,就是在损失函数中加上Lp范数。
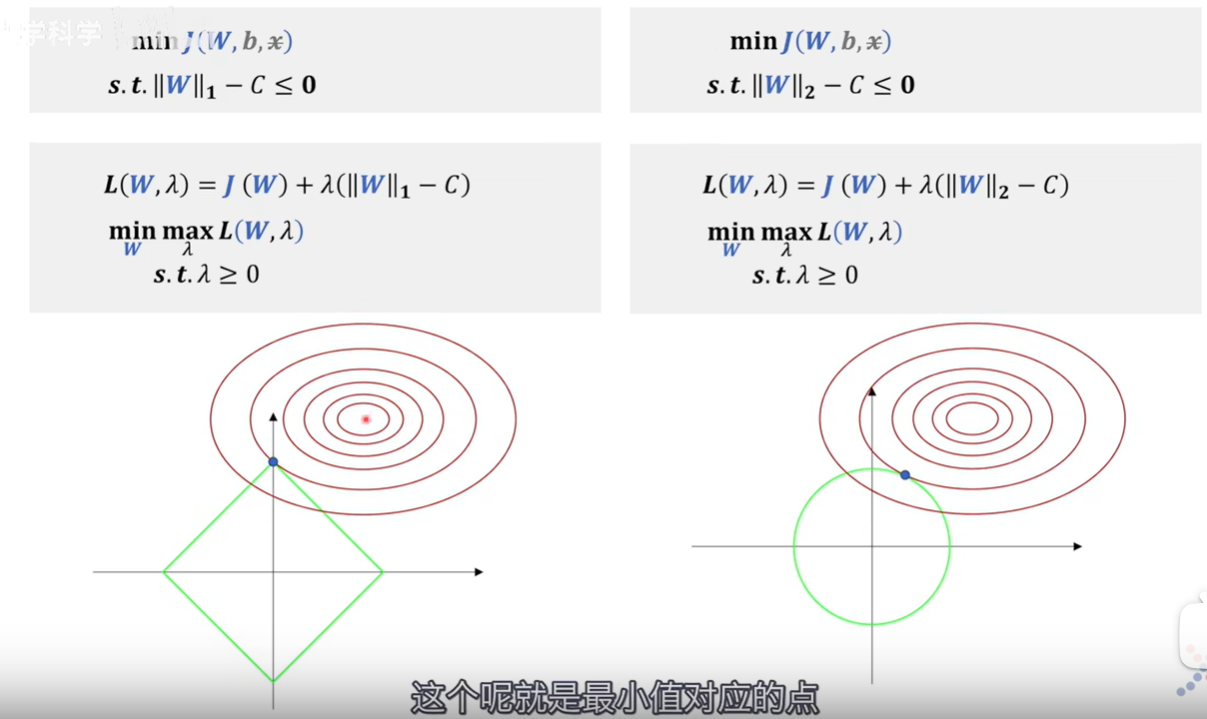
为什么说L1正则化(右)可以带来稀疏性,就是因为L1正则化后的极值点容易出现在坐标轴上,而出现在坐标轴上意味着其他某些维度的值为0,比如要用胡子和毛色区分猫咪和狗,L2正则化(左)可能只是赋予两个特征不同的权重,\(\lambda\)的作用是来调节权重大小,而L1正则化就可能只考虑胡子,而不考虑毛色,这就带来了稀疏性。·+ \(x\)是训练集里面的数据,视作常数不考虑;真正决定拟合效果的是权重\(W\),所以偏置\(b\)虽然是未知参数也不进行研究; \[ \|W\|_1-C \leq \mathbf{0} \] 这里可以理解为只考虑对\(W\)的可行域范围进行约束 。
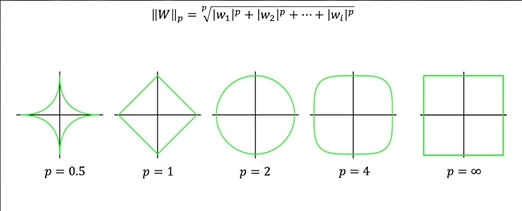
只有p>=1的时候,Lp范数才是一个凸集,这时候以Lp范数作为约束的问题才能是一个凸优化问题;反之,若0<p<1,集合就是非凸集。
我们看到的L2正则化的函数和原问题的拉格朗日函数之间的关系
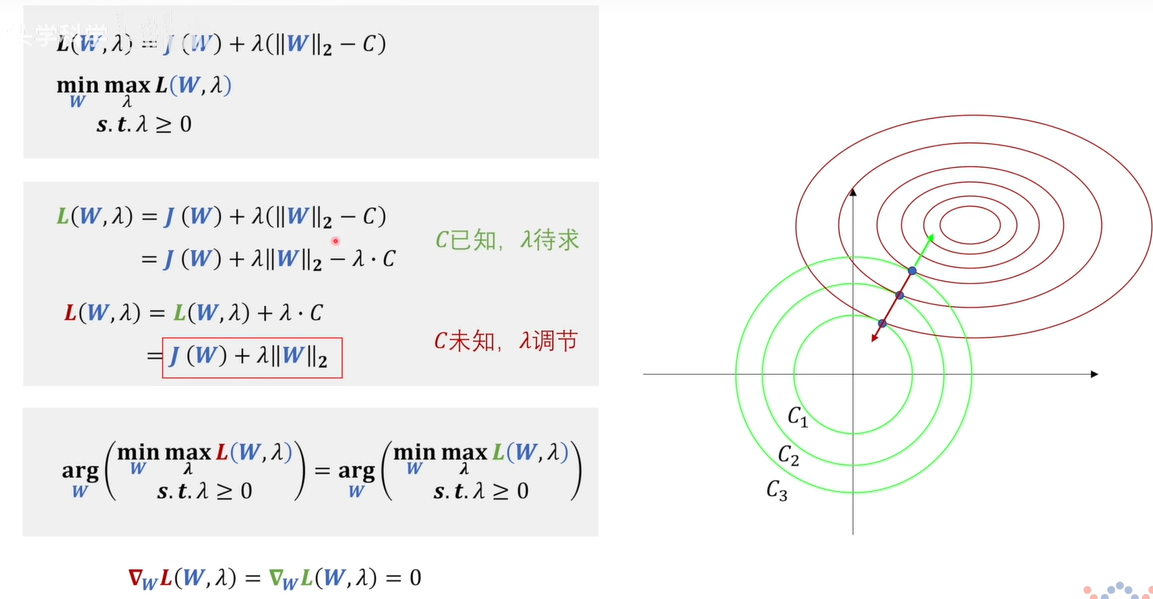
在这个问题中,红的的函数与绿色相比,少了一个\(\lambda\)\(C\),这个C其实调节的是圆半径的大小,在绿色函数中,就是C视为已知,来求\(\lambda\);而在红色函数中,是用\(\lambda\)来调节圆的半径,每一个极值点都对应一对共线相反大小相等的梯度,对应一个特别的\(\lambda\),也就是对应一个半径C(即可以通过调节\(\lambda\)来调节\(C\)。
红色和绿色两个函数对\(W\)求梯度后,得到的W值是相等的,因为\(\lambda\)\(C\)在对\(W\)求导的时候为0。看似这两个问题是等价的,但是其实超参数已经改变了,上面的超参数是\(C\),下面的是\(\lambda\)。
L1正则化和L2正则化的特性:
L1正则化会带来稀疏性。(待补充)
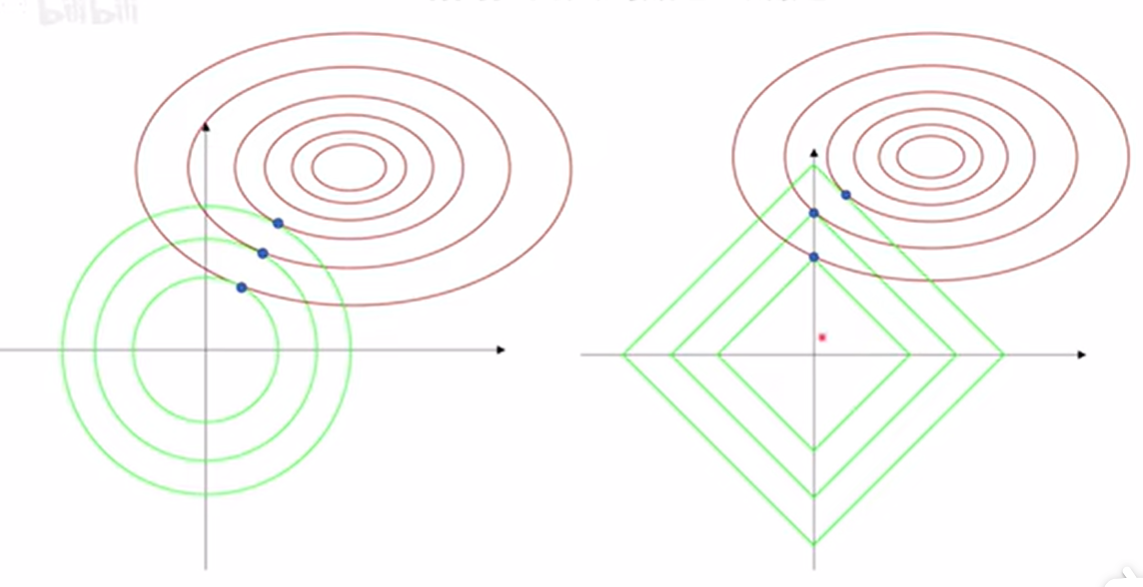
为什么说L1正则化(右)可以带来稀疏性,就是因为L1正则化后的极值点容易出现在坐标轴上,而出现在坐标轴上意味着其他某些维度的值为0,比如要用胡子和毛色区分猫咪和狗,L2正则化(左)可能只是赋予两个特征不同的权重,\(\lambda\)的作用是来调节权重大小,而L1正则化就可能只考虑胡子,而不考虑毛色,这就带来了稀疏性。
3.树模型
3.1 基础的树
李航统计学习上比较基础的树模型:ID3 C4.5 CART
三者区别:
- 划分标准的差异:ID3 使用信息增益偏向特征值多的特征,C4.5 使用信息增益率克服信息增益的缺点,偏向于特征值小的特征,CART 使用基尼指数克服 C4.5 需要求 log 的巨大计算量,偏向于特征值较多的特征。
- 使用场景的差异:ID3 和 C4.5 都只能用于分类问题,CART 可以用于分类和回归问题;ID3 和 C4.5 是多叉树,速度较慢,CART 是二叉树,计算速度很快;
- 样本数据的差异:ID3 只能处理离散数据且缺失值敏感,C4.5 和 CART 可以处理连续性数据且有多种方式处理缺失值;从样本量考虑的话,小样本建议 C4.5、大样本建议 CART。C4.5 处理过程中需对数据集进行多次扫描排序,处理成本耗时较高,而 CART 本身是一种大样本的统计方法,小样本处理下泛化误差较大 ;
- 样本特征的差异:ID3 和 C4.5 层级之间只使用一次特征,CART 可多次重复使用特征;
- 剪枝策略的差异:ID3 没有剪枝策略,C4.5 是通过悲观剪枝策略来修正树的准确性,而 CART 是通过代价复杂度剪枝。
3.2 基于集成学习的改进
基于Bagging算法典型代表
随机森林(Random Forest)
基于Boosting算法典型代表
如AdaBoost、GBDT、XGBoost等。
1)Bagging + 决策树 = 随机森林
2)AdaBoost + 决策树 = 提升树
3)Gradient Boosting + 决策树 = GBDT
那么Bagging和Boosting的区别是什么呢?
1)样本选择:
Bagging:训练集是在原始集中有放回选取的,从原始集中选出的各轮训练集之间是独立的。
Boosting:每一轮的训练集不变,只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。
基于这个性质我们可以知道,Bagging后的bias与单模型接近,而variance能显著下降,每个基模型之间是独立的。
2)样例权重:
Bagging:使用均匀取样,每个样例的权重相等
Boosting:根据错误率不断调整样例的权值,错误率越大则权重越大。
3)预测函数:
Bagging:所有预测函数的权重相等。
Boosting:每个弱分类器都有相应的权重,对于分类误差小的分类器会有更大的权重。
4)并行计算:
Bagging:各个预测函数可以并行生成
Boosting:各个预测函数只能顺序生成,因为后一个模型参数需要前一轮模型的结果。
5)适用场景:
Bagging: High Variance & Low Bias
Boosting: Low Variance & High Bias
